
 |
Siempre Scout
|
Vereda recorrida: Home - Biblioteca - Indice
Proyecciones Diversas
Si de pronto, al estar excursionando tú solo o con tu patrulla se sienten perdidos, pero disponen de un mapa del área en que se encuentran, equivaldría a que estuvieran viendo el terreno desde un helicóptero, suspendidos a 1 500 m de altura.
Desde ahí podrías ver los ríos, montañas, edificaciones, bosques y demás objetos notables. Viendo lo que te rodea, podrás identificar el lugar en que te encuentras y sobe el mapa podrías diseñar el mejor camino hasta el lugar al que deseas llegar.
En realidad, un mapa no es sino la representación casi exacta de una parte de un territorio, dibujada sobre una hoja de papel.
| ¿Qué es lo que tú deseas obtener de un mapa? | |
| | Que cada punto del terreno se pueda situar sobre el mapa. |
| | Que se pueda medir la distancia entre dos puntos. |
| | Que permita medir el rumbo entre dos puntos, para poder viajar con seguridad de uno a otro. |
| | Que permita tener una visión clara del relieve para ver la facilidad de acceso, y que permita calcular la pendiente y altitud de un punto. |
| | Que permita visualizar los obstáculos creados por la naturaleza o el hombre, para buscar la mejor ruta a un lugar dado. |
Un buen mapa debe resolver tus necesidades anteriores, pero el topógrafo tiene otros problemas para realizar el mapa que resuelva los tuyos; entre ellos, tenemos los siguientes:
1er. problema.- Como la tierra es una esfera, hay que representar una porción de ella en un plano, con la menor deformación
2o. problema.- Hay que representar todas las irregularidades del terreno modeladas por la naturaleza, como las montañas, valles y cañadas.
3er. problema.- Se deben marcar sobre el mapa, una malla o marcas de referencia, para ayudar en la ubicación exacta de todos los puntos sobre el mapa.
4o. problema.- Es necesario representar sobre el mapa todos los detalles notables del terreno, ya sean naturales como: bosques, ríos o lagos; o hechos por el hombre como: pueblos, carreteras, puentes y líneas de conducción.
El topógrafo se vale de la geometría y del uso de signos convencionales, para resolver estos problemas.
Para resolver el 1er. problema, imagínate que le quitas la cáscara a una naranja, y que tratas de extenderla sobre una superficie plana, pero sin deformarla.
Es obvio que la mejor representación de la tierra sería haciendo una esfera, pero si tomamos en cuenta que deseamos observar algunos pequeños detalles, el tamaño de nuestro mapa sería enorme.
Si por otro lado, deseáramos observar también el detalle del relieve, sería más complicada la cosa. Es por esto, que la forma más sencilla para hacer un mapa, es hacerlo sobre una superficie plana, sobre todo cuando se trata de reproducir una pequeña parte del terreno.
Hacer un mapa pequeño de una región no es mucho problema, pero si tratamos de unirlo a otros mapas de regiones vecinas para hacer una representación de una área mayor, habrá que tener alguna forma de empatarlos sin distorsiones.
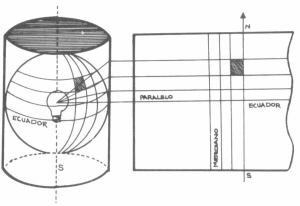
Como referencias para todos los mapas, se acostumbran utilizar líneas de referencia fijas como son los meridianos, los paralelos y además los polos y el ecuador.
| Eje Terrestre Polo Norte Polo Sur Meridianos Paralelos Ecuador |
A B C D E F |
 |
| Los meridianos son semicírculos, que partiendo de un polo al otro,
tocan al ecuador en su parte media.
Los paralelos, son líneas en forma de círculos concéntricos, vistas desde los polos y el mayor de ellos forma el ecuador. Los polos son puntos fijos, por donde se supone que pasa el eje sobre el que gira la tierra. Otra referencia fija, es el nivel del mar, al cual se refieren todas las altitudes y que son proyectadas hacia el mismo, siguiendo una línea vertical, la que si se prolongara, llegaría al centro de la tierra. |
 |
|
|
| La superficie del nivel del mar también es curva, por lo que
habrá que hacer otra proyección hacia un plano por lo que
habrá otra distorsión. Es imposible evitar estos errores, pero
para pequeñas superficies, el error es muy pequeño.
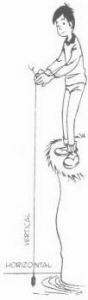
Una dirección vertical es la que indica un hilo de una plomada y una dirección horizontal se considera la que indica la superficie del agua en reposo. Estas direcciones están consideradas como perpendiculares entre sí, en pequeñas extensiones del terreno. |
Hemos visto que para territorios pequeños, no existen grandes distorciones debidas a la proyección, pero cuando se trata de extensiones grandes como las de un país, un continente o de todo el globo, se requieren otros tipos de proyecciones, que eviten al mínimo la distorsión.
Si consideramos a la tierra como un globo transparente y en el centro de la misma colocáramos una lámpara, si colocamos alrededor del globo un cilindro semi-transparente, veríamos que los meridianos son proyectados como líneas verticales colocadas a la misma distancia entre sí; en cambio, los paralelos también aparecerían como líneas paralelas horizontales entre sí, pero se irían separando al avanzar desde el ecuador a los polos, distorsionando enormemente las regiones cercanas a los polos, haciéndolas aparecer mayores de lo que son en realidad.
La proyección de Mercator es por lo tanto muy útil para representar casi todo el globo en un plano, pero no puede representar las regiones polares. Por otro lado, sólo se considera exacta en las regiones cercanas al ecuador.
Si en lugar de proyectar sobre el cilindro semitransparente a todos los paralelos y meridianos, partiendo del centro de la tierra como en la proyección de Mercator, los proyectamos desde el eje terrestre y perpendiculares a él, obtenemos una proyección en la cual los paralelos aparecen como líneas paralelas y equidistantes pero ahora los meridianos aparecen como líneas paralelas que se van acercando entre sí, conforme nos alejamos del ecuador hacia los polos.
Otro tipo común de proyección global es la que se obtendría viendo a la tierra desde el espacio a una gran distancia desde una nave espacial, pero sólo muestra la mitad de la cara de la tierra.
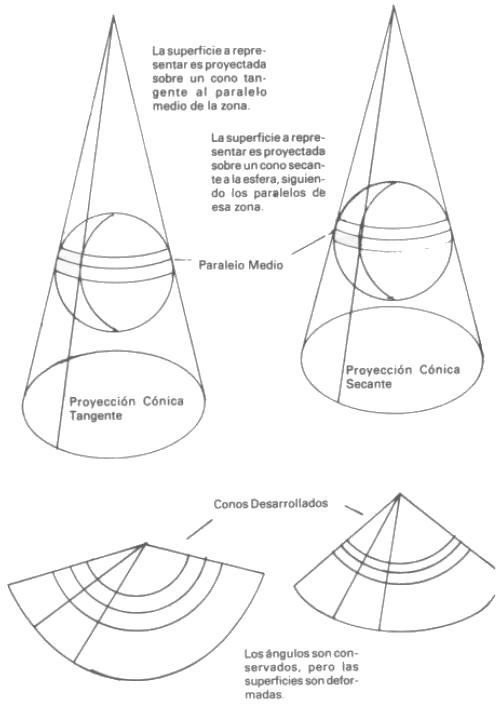
Cuando se trata de representar extensiones grandes, como un país o un continente, pero no todo el globo, se utilizan proyecciones hechas sobre planos o secciones de un cono, por ser más fáciles de realizar y representan algunas ventajas.
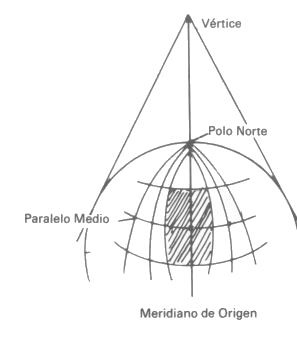
Proyección de Bonne
La proyección de Bonne proyectada
|
 |
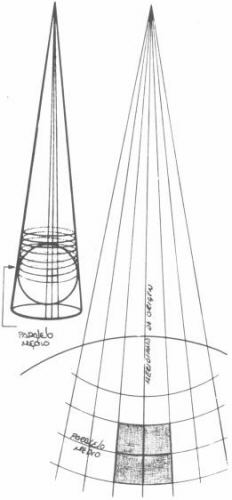 |
Proyección de LambertLa proyección de Lambert es una variante mejorada de la proyección cónica. Está basada en la proyección de una porción de territorio sobre un cono que tiene su cúspide más alta que su base, que es tangente al paralelo medio de la región. Dos convenciones que perfeccionan y complementan a una proyección simple son: 1a.- Los meridianos están representados por líneas que, partiendo de la cúspide del cono, cortan al paralelo medio en el punto donde el cono de desarrollo es tangente al meridiano que representa. Las deformaciones en longitud son nulas sobre el paralelo de origen pero aumentan rápidamente cuando uno se aleja hacia el norte o sur del mismo. 2a.- Los paralelos se representan por círculos concéntricos que parten de la cúspide del cono. Los mapas de la República Mexicana que edita el Instituto Nacional de Estadística, Geografía e Informática, (INEGI) que depende de la Secretaría de Programación y Presupuesto a una escala de 1:5000,000, utilizan este tipo de proyección. |
En pequeñas porciones de terreno se utilizan planos topográficos, en los que no aparece la redondez de la tierra como un dato importante. Sin embargo, para unir varios planos y que haya correspondencia entre ellos, se utiliza comúnmente la proyección de Mercator, pero modificándola, para sacar ventaja del hecho que no deforma grandemente a las regiones cercanas al ecuador.
Proyección Universal Transversa de Mercator |
|
|
La figura 1 muestra la proyección
convencional de Mercator como la hemos visto; en la figura 2 aparece la
proyección transversa, o sea la proyección no del ecuador,
sino de un meridiano cualquiera.
Si proyectamos únicamente una área de 3 grados a los lados del meridiano medio como en la figura 3, las áreas representadas tienen muy poca deformación.
La tierra está recortada en 60 husos de 6º. Cada huso posee su meridiano medio (línea punteada). |
| En lugar de ser tangente al ecuador (1) el cilindro es tangente al meridiano (2) | |
|
|
En esta forma obtenemos la proyección de un gajo de 6º de ancho únicamente, pero si hacemos girar 60 veces al cilindro, obtenemos la proyección de toda la tierra, como vemos en la figura 4.
El cilindro (A, B. C) gira alrededor de la tierra 60 veces para formar los husos (A, B, C).
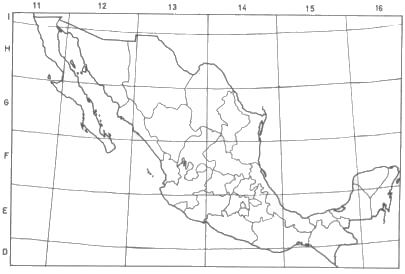
La República Mexicana está comprendida entre los gajos o husos del 11 al 16, con paralelos medios de 117º, 111º, 105º, 99º 93º y 87º.
Los mapas de la República a una escala de 1:50,000 son parte de una proyección de este tipo. Cada huso se divide en cuadros de 4º de latitud, o sea que abarcan una superficie comprendida entre 6º de longitud por 4º de latitud.
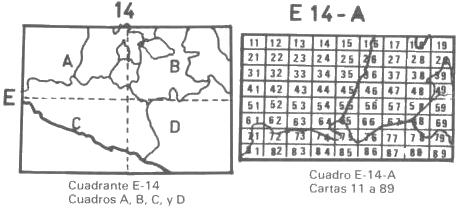
Cada uno de estos cuadros, se subdivide a su vez en cuatro cuadrantes de 3º por 2º, denominados con las letras A, B, C, y D.
Por último, los cuadrantes están formados por "cartas" que abarcan únicamente 20 minutos de longitud por 15 de latitud.
Para escoger un mapa, hay que considerar su escala
Para que un mapa sea útil al excursionista, se debe de tomar en cuenta su escala.
Los mapas son una representación del terreno a una escala reducida para hacerlos transportables, con la condición que en todo el mapa se conserva la misma escala.
La escala del mapa, es la relación constante entre las dimensiones sobre el terreno y las dimensiones sobre el mapa.
Es muy importante pues, que los mapas incluyan este dato; así hablamos de un mapa a una escala de 1 :500,000 o de otro a una escala de 1:200,000.
En un mapa de 1:50,000 un cm. del mapa representa a 50,000 cm. del terreno, en uno de escala 1:200,000 un cm. representa 200,000 cm. o dicho de otra manera, cambiando unidades, 500 m en el primero y 2,000 m en el segundo.
La escala está impresa en los mapas en forma de una fracción como:
1:20,000, 1:50,000 ó 1:250,000 por ejemplo. Cuando el denominador es muy grande, la escala es pequeña y el mapa no contiene detalles pequeños; sin embargo, si el denominador es pequeño, la escala es mayor y se pueden anotar detalles pequeños dentro del mapa, por ejemplo si la escala es de 1 :2,000, un cm. del mapa, representa a 20 m sobre el terreno.
Para utilizar la escala del mapa, es necesario hacer algunos cálculos simples, pero conviene recordar que si corremos el punto decimal tres lugares a la izquierda, la distancia medida en mm sobre el mapa, nos dará la distancia real en metros sobre el terreno.
| Por ejemplo: | a 1:5,000 a 1:50,000 a 1:250,000 |
1 mm representa 5 m 1 mm representa 50 m 1 mm representa 250 m |
Para escoger la escala del mapa, se tendrá en cuenta el uso que se va a dar al mismo. Los mejores mapas para excursionar son los de escala de 1:50,000 o escalas menores si los hay disponibles (1:25,000 ó 1:20,000).
Los pilotos que viajan a 500 km por hora no necesitan de los pequeños deta!les, por lo que utilizan por lo regular escalas de 1:250,000 o mayores, en las cuales se destaca el relieve y se marcan altitudes, posición de radiofaros, áreas peligrosas o restringidas, aeropuertos, luces de situación, pasillos de circulación aérea, o sea los datos importantes para su seguridad.
En un mapa pequeño de 50x80cm, con escala de 1:1000,000, se cubren unos 400,000 km2.
En los mapas de carreteras se marcan los datos importantes para un automovilista y por lo regular no se indican las subidas o las bajadas, ya que el motor se encarga del trabajo.
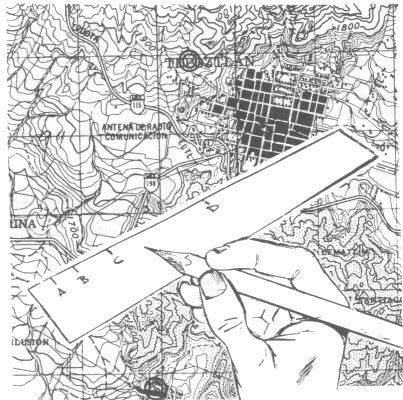
Para calcular la distancia a recorrer sobre un mapa, es conveniente hacer una reglilla con una copia de la escala gráfica que aparece en muchos mapas, en forma de una línea marcada en metros o kilómetros, hecha en una tira de cartulina.
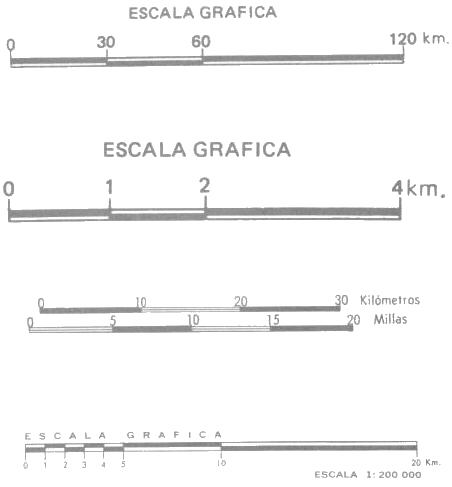
Pero cuando uno está excursionando en el campo, sin instrumentos de medición para medir distancias reales, la forma más sencilla y barata es contando el número de pasos que damos al hacer un recorrido; este método, aunque es aparentemente burdo, tiene una exactitud de un 2%, y fue usado desde épocas tan remotas como en las culturas griegas y romanas.
Para usar esta técnica, se recorre una distancia conocida varias veces y se cuenta únicamente cada dos pasos sencillos, o sea cada que el talán del pie izquierdo toca el suelo. Por ejemplo, en 100 m se dan 60 doble pasos. Esta medida se coloca junto a la escala gráfica en una reglilla de cartulina para hacer mediciones directas en el mapa, sin necesidad de hacer cálculos.
Cómo se mide la longitud total de un recorrido sobre el mapa:
1) A un lápiz duro, se le saca punta muy aguda.
2) Cortar una tira de cartulina o papel bristol blanco.
3) Colocar la tira de papel en tramos rectos sobre el camino a recorrer, añadiendo cada tramo a continuación del anterior, para obtener el largo total.
4) Al llegar al final del recorrido, compara la tira con la escala gráfica que se encuentra en tu mapa, así podrás conocer directamente la distancia por recorrer.
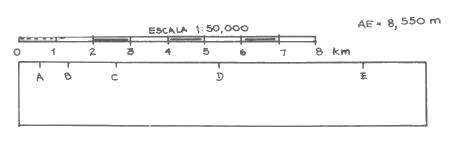
Si te gustan las matemáticas, mide la distancia en cm y mm para que hagas el cálculo de la distancia con mayor exactitud y así podrás comprobar el resultado.
Las distancias así medidas no son reales ya que no tomamos en cuenta las diferencias de nivel y pequeños rodeos para evitar obstáculos, a menos que seas pájaro o vueles en helicóptero. El recorrido total será un poco mayor en realidad, pero el medir sobre el mapa te da una buena idea del camino a recorrer.
Arriba |
Siguiente |